數學可以變成藝術
數學考題寫不出來,是許多人難忘的痛苦經歷。數學真的那麼討人厭嗎?數學家李國偉為數學「平反」,他認為數學讓學生討厭,是因為現行的教育多強調「解難題」。當難題解不出來,就會開始懷疑:數學到底可以做什麼?

圖│研之有物
非常簡單的操作,反覆使用的時候,表象就變得非常複雜。這給我們很深刻的哲學啟示:宇宙看起來這麼複雜,可是它後面的真理說不定很簡單。
數學刺激藝術,藝術又刺激數學。現代電腦影響人們的思維,許多當代藝術融入理性化的幾何圖形,例如克卜勒星形正多面體的公共雕塑。另外,從摺紙藝術延伸,現今航太科技也運用「摺紙工程」,利用摺痕來增加紙張材料的強度、節省運送空間與重量。一張紙如何摺才能達到目的,這也需要數學來計算。

圖│研之有物
古老數學遊戲藏著大學問
數學除了成為「藝數」,也可以用來玩遊戲。有一類組合優化問題,目前還沒有解決,成為懸賞 100 萬美元的 21 世紀七大數學難題之一。
李國偉說,這類難題源自於 19 世紀漢彌爾頓 (William Rowan Hamilton) 發明的「環遊世界」數學遊戲 (Icosian Game):把一個正 12 面體的 20 個頂點分別標上倫敦、巴黎、北京、東京、華盛頓等 20 個大都市的名字,要求玩的人從某個城市出發、沿著正 12 面體的稜邊,通過每 1 個城市只能 1 次,最後再回到出發的城市。
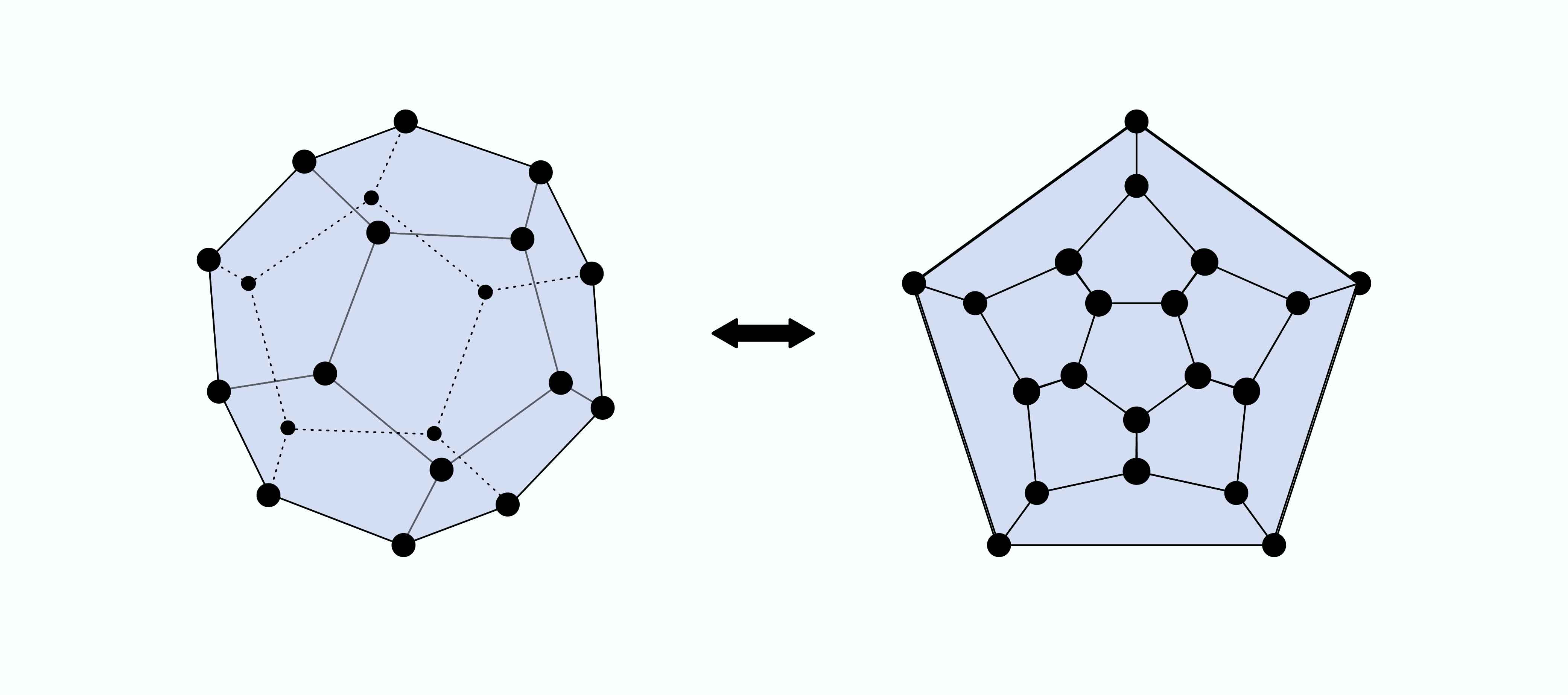
圖│Hamiltonian Graph
圖論 (Graph Theroy)是什麼呢?簡單說就是透過點、線的組合,找出最省時間空間的答案。
李國偉致力於圖論的研究,其中一個重要的問題是「著色理論」:如何用最少的顏色,將一張圖上的所有頂點上色,且相連接的頂點不能同色。
李國偉說明,這種組合數學的問題,答案一定存在,但是實際求解的時候,希望找到最有效率、最節省資源的解,這就是「組合優化」的問題。當然可以每個點都塗不同顏色,但如此一來就用掉太多顏色。這類問題更進一步成為計算機科學裡面「演算法」的學問。
圖論也可以換個形式,在各個點填入數字,變成訓練理解「離散數學」的模型工具,在各個分散的數字中,尋找有特殊結構的集合。李國偉也鑽研數學史,發現有趣的「離散數學」案例,來自清末太平天國時期保其壽《碧奈山房集》書中的「六道渾天圖」。這種圖形充滿神秘感,如同西方的魔方陣 (magic square) 蘊藏數學的構造原理。

圖│論保其壽的渾圓圖,作者:李國偉
「六道渾天圖」用六條紙帶互相穿插,交錯成許多三角形與五邊形構成的十二并二十面體,目標是把 91 個數字分別填入圖形的頂點與邊線,使得每個三角形周邊數字總和相同,每個五邊形周邊數字總和也相同。李國偉認為「六道渾天圖」並不是老掉牙的古籍記載而已,它可刺激新的組合數學研究,例如推廣到其他規則圖形上複雜的定和標數。
19 世紀的西方數學非常發達,雖然西方也有人用心於創作魔方陣 ,但未曾像保其壽在立方體上設計如此複雜的定和標數。「把古老的東西,用現代的數學語言去了解它,然後從它興起新的數學問題。古為今用,我覺得很有趣!」李國偉看著清末的「六道渾天圖」而發出讚嘆。
李國偉強調,數學與藝術、文化有很微妙的關聯。而他所期盼的數學課,不再只是出難題把人逼瘋,而是讓學生摺紙、動手做,不適合解題的學生也能發揮想法、獲得肯定。
最重要的是,有數學的素養,就可以欣賞更多東西,豐富我們的人生!







